Geometric analysis enables biological insight from complex non-identifiable models using simple surrogates

An enduring challenge in computational biology is to balance data quality and quantity with model complexity. Tools such as identifiability analysis and information criterion have been developed to harmonise this juxtaposition, yet cannot always resolve the mismatch between available data and the granularity required in mathematical models to answer important biological questions. Often, it is only simple phenomenological models, such as the logistic and Gompertz growth models, that are identifiable from standard experimental measurements.

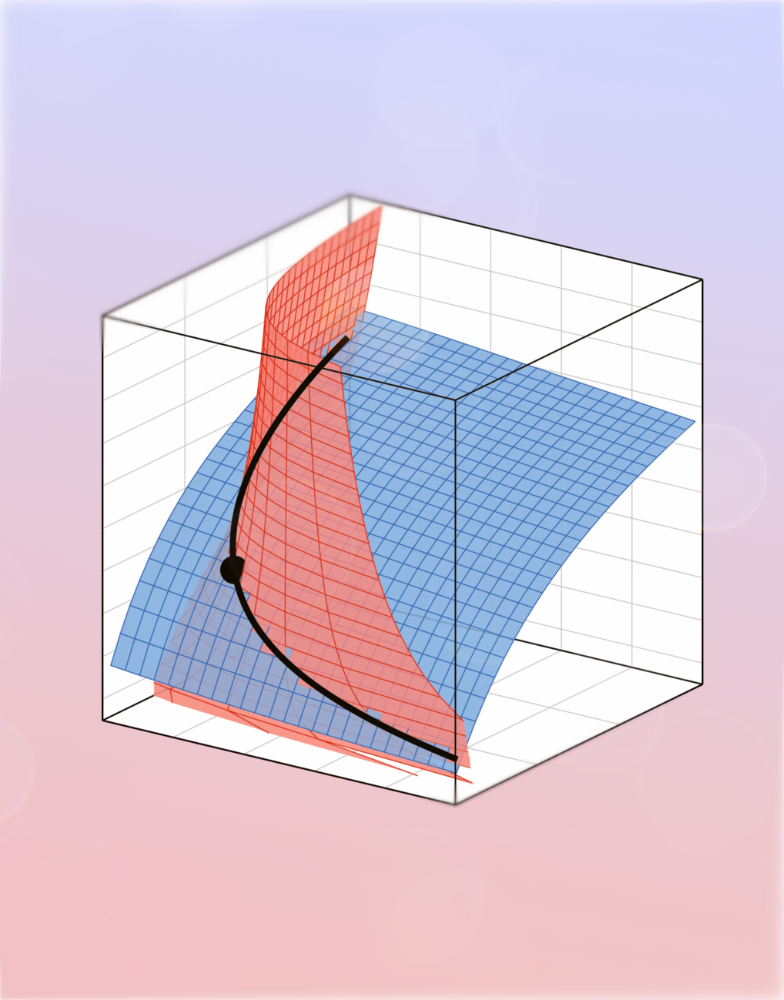
To draw insights from the complex, non-identifiable models that incorporate key biological mechanisms of interest, we study the geometry of a map in parameter space from the complex model to a simple, identifiable, surrogate model. By studying how non-identifiable parameters in the complex model quantitatively relate to identifiable parameters in surrogate, we introduce and exploit a layer of interpretation between the set of non-identifiable parameters and the goodness-of-fit metric or likelihood studied in typical identifiability analysis. We demonstrate our approach by analysing a hierarchy of mathematical models for multicellular tumour spheroid growth. Typical data from tumour spheroid experiments are limited and noisy, and corresponding mathematical models are very often made arbitrarily complex. Our geometric approach is able to predict non-identifiabilities, subset non-identifiable parameter spaces into identifiable parameter combinations that relate to individual data features, and overall provide additional biological insight from complex non-identifiable models.