A Bayesian computational approach to explore the optimal duration of a cell proliferation assay

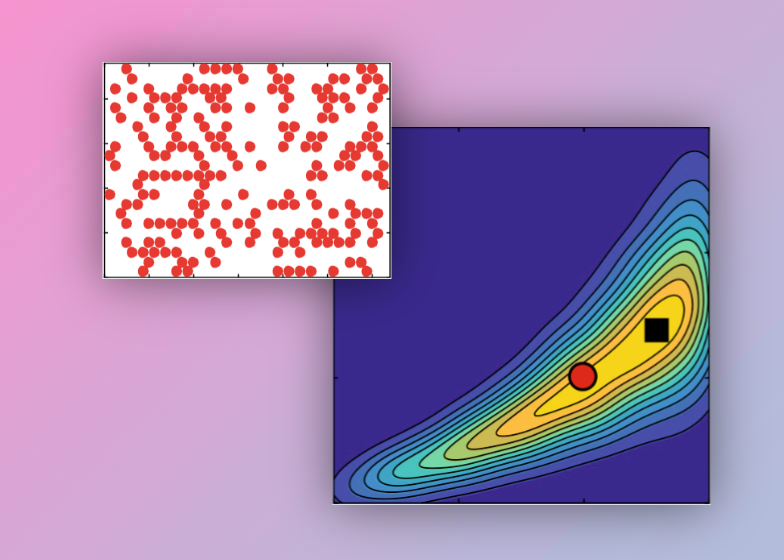
Cell proliferation assays are routinely used to explore how a low density monolayer of cells grows with time. For a typical cell line with a doubling time of 12 hours (or longer), a standard cell proliferation assay conducted over 24 hours provides excellent information about the low-density exponential growth rate, but limited information about crowding effects that occur at higher densities. To explore how we can best detect and quantify crowding effects, we present a suite of in silico proliferation assays where cells proliferate according to a generalised logistic growth model. Using approximate Bayesian computation we show that data from a standard cell proliferation assay cannot reliably distinguish between classical logistic growth and more general non-logistic growth models. We then explore, and quantify, the trade-off between increasing the duration of the experiment and the associated decrease in uncertainty in the crowding mechanism.