Profile likelihood analysis for a stochastic model of diffusion in heterogeneous media
MJ Simpson, AP Browning, C Drovandi, EJ Carr, OJ Maclaren, RE Baker
Proceedings of the Royal Society A (2021)
MJ Simpson, AP Browning, C Drovandi, EJ Carr, OJ Maclaren, RE Baker
Proceedings of the Royal Society A (2021)
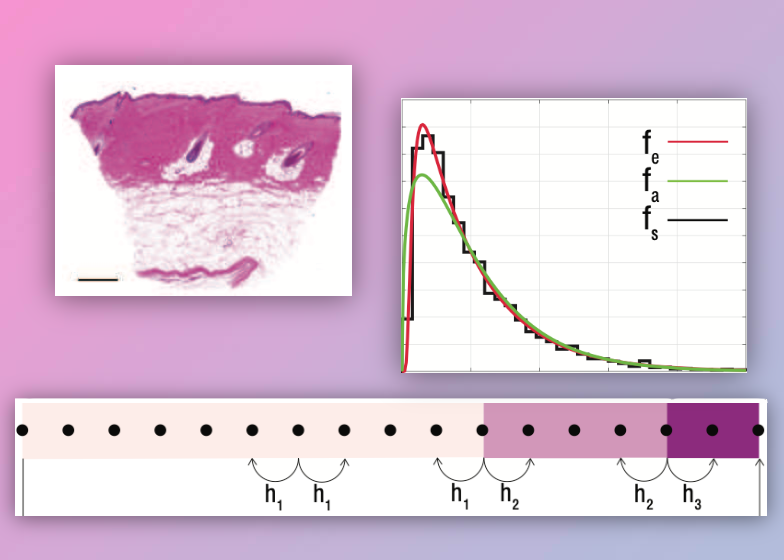
We compute profile likelihoods for a stochastic model of diffusive transport motivated by experimental observations of heat conduction in layered skin tissues. This process is modelled as a random walk in a layered one-dimensional material, where each layer has a distinct particle hopping rate. Particles are released at some location, and the duration of time taken for each particle to reach an absorbing boundary is recorded. To explore whether these data can be used to identify the hopping rates in each layer, we compute various profile likelihoods using two methods: first, an exact likelihood is evaluated using a relatively expensive Markov chain approach; and, second, we form an approximate likelihood by assuming the distribution of exit times is given by a Gamma distribution whose first two moments match the moments from the continuum limit description of the stochastic model. Using the exact and approximate likelihoods, we construct various profile likelihoods for a range of problems. In cases where parameter values are not identifiable, we make progress by re-interpreting those data with a reduced model with a smaller number of layers.