Model-based data analysis of tissue growth in thin 3D printed scaffolds
AP Browning, OJ Maclaren, PR Buenzli, M Lanaro, MC Allenby, MA Woodruff, MJ Simpson
Journal of Theoretical Biology (2021)
AP Browning, OJ Maclaren, PR Buenzli, M Lanaro, MC Allenby, MA Woodruff, MJ Simpson
Journal of Theoretical Biology (2021)
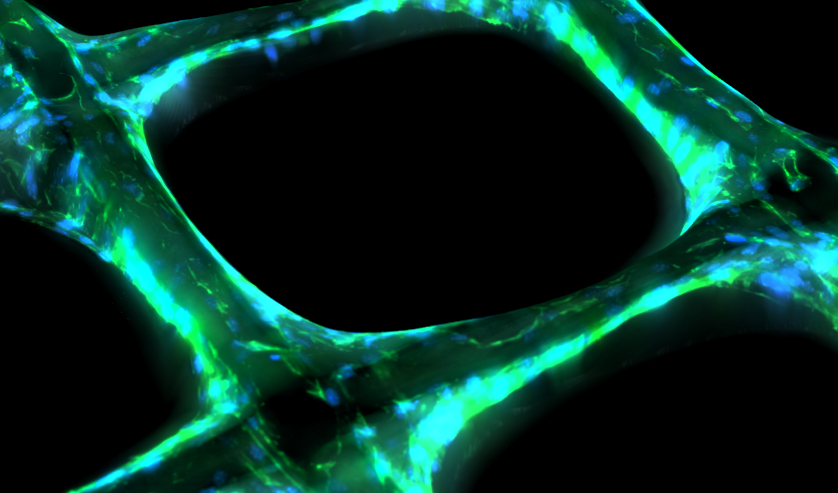
Tissue growth in three-dimensional (3D) printed scaffolds enables exploration and control of cell behaviour in biologically realistic geometries. Cell proliferation and migration in these experiments have yet to be explicitly characterised, limiting the ability of experimentalists to determine the effects of various experimental conditions, such as scaffold geometry, on cell behaviour. We consider tissue growth by osteoblastic cells in melt electro-written scaffolds that comprise shallow square pores with sizes that we deliberately vary. We collect highly detailed temporal measurements of the average cell density, tissue coverage, and tissue geometry. To quantify tissue growth in terms of the underlying cell proliferation and migration processes, we introduce and calibrate a mechanistic mathematical model based on the Porous-Fisher reaction-diffusion equation. Parameter estimates and uncertainty quantification through profile likelihood analysis reveal consistency in the rate of cell proliferation and steady-state cell density between pore sizes. This analysis also serves as an important model verification tool: while the use of reaction-diffusion models in biology is widespread, the appropriateness of these models to describe tissue growth in 3D scaffolds has yet to be explored. We find that the Porous-Fisher model is able to capture features relating to the cell density and tissue coverage, but is not able to capture geometric features relating to the circularity of the tissue interface. Our analysis identifies two distinct stages of tissue growth, suggests several areas for model refinement, and provides guidance for future experimental work that explores tissue growth in 3D printed scaffolds.